Qualificador da Índia para Pokémon Unite World Championship 2025 anunciou

Após o torneio de inverno, a jornada para Anaheim está em andamento e, para as equipes indianas do Pokémon Unite, as apostas nunca foram mais altas. A Pokémon Company e a Skyesports divulgaram o qualificador da Índia para a série Pokémon Unite World Championship 2025. Este evento não apenas possui um consultório alto de US $ 37.500, mas também oferece a oportunidade de ouro para o vencedor representar a Índia no palco global no WCS 2025 na Califórnia.
As inscrições para as qualificadoras da Índia estão atualmente abertas e serão encerradas em 4 de abril. A competição começa em 5 de abril, estruturada como um suporte de eliminação única. As oito principais equipes progredirão para os playoffs em 6 de abril, onde o formato muda para um suporte de eliminação dupla, dando às equipes uma segunda chance mesmo após uma derrota.
Cada partida seguirá o melhor de três do formato, garantindo que as equipes tenham ampla oportunidade de ajustar suas estratégias e superar seus rivais. O ritmo rápido do torneio promete confrontos emocionantes, mas com apostas tão altas, o planejamento estratégico meticuloso será crucial.

A equipe que emerge vitoriosa não apenas garantirá uma parcela significativa do prêmio em dinheiro, mas também ganhará o prestigiado direito de representar a Índia no Pokémon Unite World Championship 2025 em Anaheim, Califórnia. É aqui que a elite mundial competirá pelo título final e uma fatia do prêmio global de US $ 500.000.
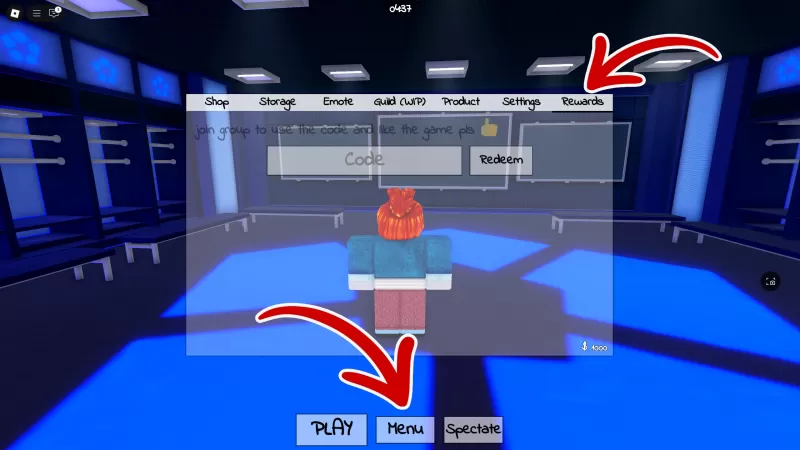
Resgate Estes códigos une-uns Pokémon para desfrutar de algumas recompensas gratuitas no jogo!
Shiva Nandy, fundador e CEO da Skyesports, expressou sua emoção sobre o torneio, afirmando: "Após o tremendo sucesso da Liga da ACL India 2025, que atraiu mais de 1,3 milhão de visualizações, estamos emocionados com a base de que os curtidores do Pokémon unem a grama e os que estão em busca de um dos mais importantes. Muitas felicidades a todos os participantes. "
-
 Chess Endgame StudiesCom base nos melhores estudos de xadrez, particularmente selecionados para seu valor instrutivo, este curso de treinamento representa um subconjunto especializado do renomado curso de CT-Art 4.0. Não há alternativa quando se trata da simplicidade e excelência dos estudos apresentados, muito menos de sua beleza atemporal
Chess Endgame StudiesCom base nos melhores estudos de xadrez, particularmente selecionados para seu valor instrutivo, este curso de treinamento representa um subconjunto especializado do renomado curso de CT-Art 4.0. Não há alternativa quando se trata da simplicidade e excelência dos estudos apresentados, muito menos de sua beleza atemporal -
 Táticas no Xadrez Vol. 2Desbloqueie seu potencial de xadrez com a segunda parte do nosso curso abrangente projetado especificamente para jogadores do clube. Essa parte enriquecedora da série possui mais de 2600 exercícios, com mais de 400 exemplos detalhados para explorar e 2200 problemas desafiadores a serem resolvidos. Esses exercícios são M
Táticas no Xadrez Vol. 2Desbloqueie seu potencial de xadrez com a segunda parte do nosso curso abrangente projetado especificamente para jogadores do clube. Essa parte enriquecedora da série possui mais de 2600 exercícios, com mais de 400 exemplos detalhados para explorar e 2200 problemas desafiadores a serem resolvidos. Esses exercícios são M -
 Capturing Pieces 1 (Chess)Este curso oferece mais de 1400 exercícios projetados com um número limitado de peças no quadro, tornando -o um recurso inestimável para iniciantes de xadrez que desejam aprimorar suas habilidades rapidamente. Como iniciante, é fundamental não perder suas peças em apenas um movimento se você pretende melhorar. Da mesma forma, você deve
Capturing Pieces 1 (Chess)Este curso oferece mais de 1400 exercícios projetados com um número limitado de peças no quadro, tornando -o um recurso inestimável para iniciantes de xadrez que desejam aprimorar suas habilidades rapidamente. Como iniciante, é fundamental não perder suas peças em apenas um movimento se você pretende melhorar. Da mesma forma, você deve -
 ReversiMergulhe no jogo de estratégia clássica da Reversi, agora aprimorado com uma interface de usuário impressionante e enriquecida com recursos interessantes. Se você está procurando desafiar amigos ou testar suas habilidades contra a IA, este aplicativo reversi lindamente projetado oferece uma experiência de jogo perfeita e agradável a qualquer momento
ReversiMergulhe no jogo de estratégia clássica da Reversi, agora aprimorado com uma interface de usuário impressionante e enriquecida com recursos interessantes. Se você está procurando desafiar amigos ou testar suas habilidades contra a IA, este aplicativo reversi lindamente projetado oferece uma experiência de jogo perfeita e agradável a qualquer momento -
 Ludi ClassicO jogo clássico do Caribe se prepara para uma emocionante reviravolta em um clássico amado com a chegada do clássico derivado do Caribe, Ludi Classic! Este jogo traz uma deliciosa fusão de culturas diretamente para as pontas dos dedos. Originalmente um presente da Índia para a Jamaica, Ludi é o Caribbean querido
Ludi ClassicO jogo clássico do Caribe se prepara para uma emocionante reviravolta em um clássico amado com a chegada do clássico derivado do Caribe, Ludi Classic! Este jogo traz uma deliciosa fusão de culturas diretamente para as pontas dos dedos. Originalmente um presente da Índia para a Jamaica, Ludi é o Caribbean querido -
 CELLS - Tile Matching GamesJogos correspondentes e ladrilhos Connect Rock! Aproveite a emoção de ladrilhos correspondentes e se envolver em jogos de partida que o mantêm entretido por horas. O jogo de correspondência de telha de células está emocionado em recebê -lo em um mundo maravilhoso de jogos correspondentes. Embarque em uma jornada emocionante conosco, onde uma infinidade de combinações
CELLS - Tile Matching GamesJogos correspondentes e ladrilhos Connect Rock! Aproveite a emoção de ladrilhos correspondentes e se envolver em jogos de partida que o mantêm entretido por horas. O jogo de correspondência de telha de células está emocionado em recebê -lo em um mundo maravilhoso de jogos correspondentes. Embarque em uma jornada emocionante conosco, onde uma infinidade de combinações